16 Appendix - General penalty functions

Penalty functions are used in a variety of places within ODL Live to define customised soft and hard limits based on a value. These include:

Defining hard and soft limits on the amount of time an item can be on-board a vehicle.
Setting limits or additional costs on drive time and/or km between two locations.
Maximum travel time between stops on the same route (i.e. not just consecutive stops, but restricting the geographic spread of a route to keep it in a small area).
Total travel time or km for a route.
Working time limits on a vehicle.

You can also set custom penalties based on the arrival time at a stop, which work the same way as the penalty functions (although the fields are named differently as they’re based on time).

Penalty functions are defined by an array of quadratic functions, where different functions can be used for different values of x. The quadratic function used in each element of the array is:

In this function:

x is the value the penalty function is based on (e.g. travel hours).
p(x) is the value of the penalty cost.
c₀ is a fixed cost that is always added if this penalty function is used. This field is called c0 in the JSON.
c₁ is a cost that’s multiplied by x, so if we have a penalty function where x is in units of hours, c₁ would be a cost per hour. Conversely for a penalty function that’s based on km, c₁ would be a cost per km. This field is called c1 in the JSON.
c₂ is a cost that’s multiplied by x² (i.e. the square of x), so if we have a penalty function where x is in units of hours, c₂ would be a cost per hour squared. This field is called c2 in the JSON.
translate offsets the x value that’s used. For example, if your penalty function is used for x ≥ 5 and you want an increasing linear cost for p(x) that starts at 0 when x = 5 (i.e. p(5) = 0), you could set translate = 5 and set c₁ to be any positive number. This field is called translate in the JSON.

For the mathematically-inclined reader, if we have an array of different functions, then each element in the function is called a subfunction and the whole array is called a piecewise function. The whole piecewise function is defined mathematically as:

ODL Live has a tool in the software developer’s dashboard that helps you configure penalty functions. Go to ODL Live’s dashboard, click on the Model editor link, then click on the Tools link, and finally click on the View penalty functions link (if not already selected). Enter the following JSON into JSON editor on the left (if not already there).

[
  {
    "inclusiveLowerLimit": 0,
    "c1": 1
  }
]

Next click the Update graph button to update the graph. Your screen should look similar to:

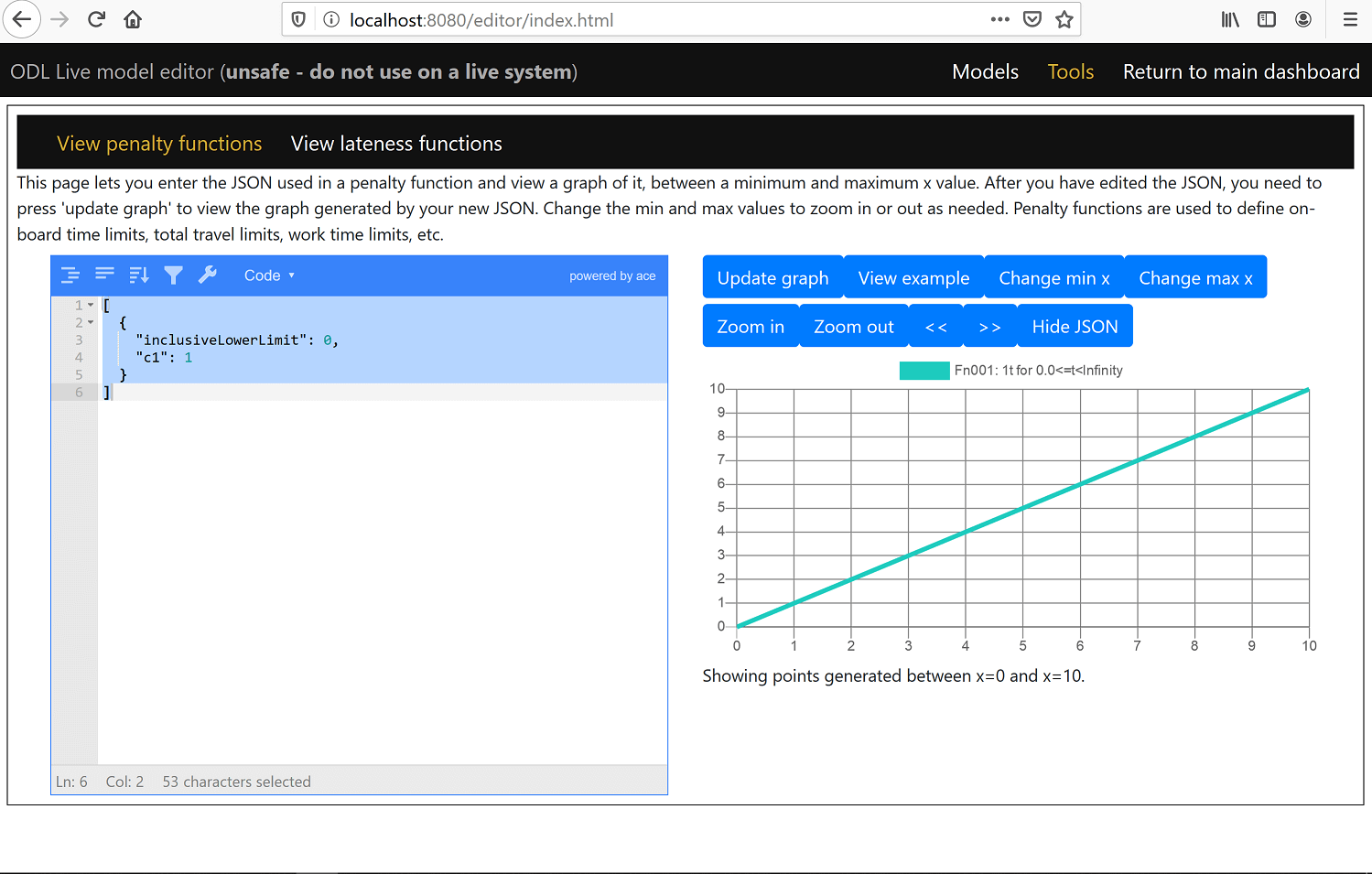
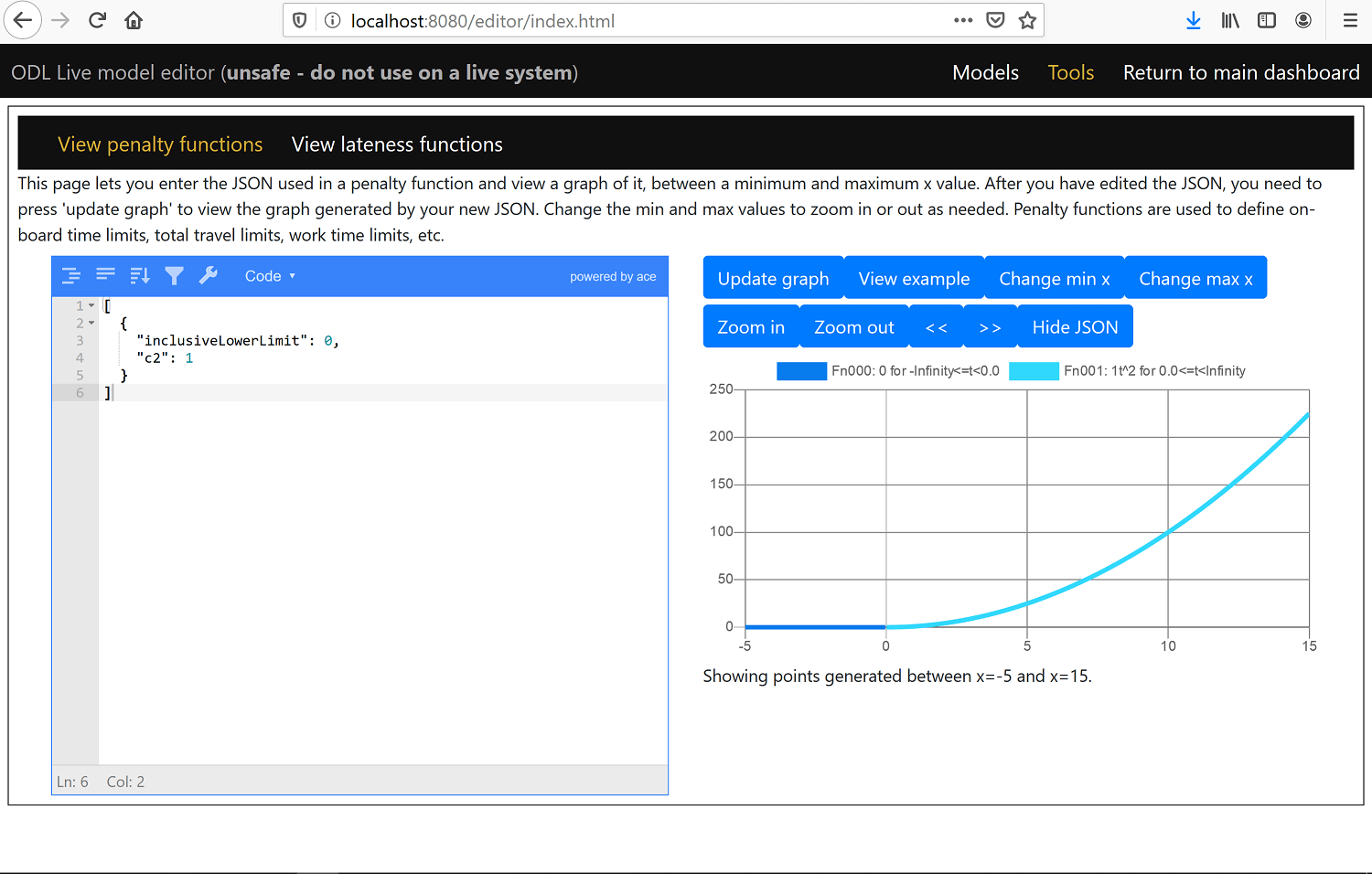
This is a simple linear function where x increases from 0. If you change the field c1 in the JSON editor to c2 instead and press the Update graph button, then you get a function that increases as the square of x from x = 0 onwards. If you press Zoom out, you see that the value is 0 for x < 0:

Now let’s try a piecewise function. Enter the following JSON:

[
  {
    "inclusiveLowerLimit": 0,
    "c1": 1
  },
  {
    "inclusiveLowerLimit": 5,
    "c2": 1
  }
]

Here we have a 1st subfunction which is linear (p(x) = c₁x for 0 ≤ x < 5) and a 2nd subfunction which is squared (p(x) = c₂x² for 5 ≤ x < ∞). The values of inclusiveLowerLimit define when the 1st subfunction and 2nd subfunctions start. We don’t need to set when each subfunction ends as ODL Live assumes the 1st subfunction ends when the 2nd subfunction starts. It also assumes (a) the last subfunction ends at infinity and (b) p(x) is 0 for all values of x before the inclusiveLowerLimit of the 1st subfunction. The values which are missing from the function - e.g. c₀, c₂, translate in the 1st subfunction - are always assumed to be 0. When defining multiple subfunctions, the subfunctions should be in increasing order of inclusiveLowerLimit (i.e. a subfunction earlier in the array should always have inclusiveLowerLimit lower than a subfunction later in the array).

Next press Update graph to view this function:

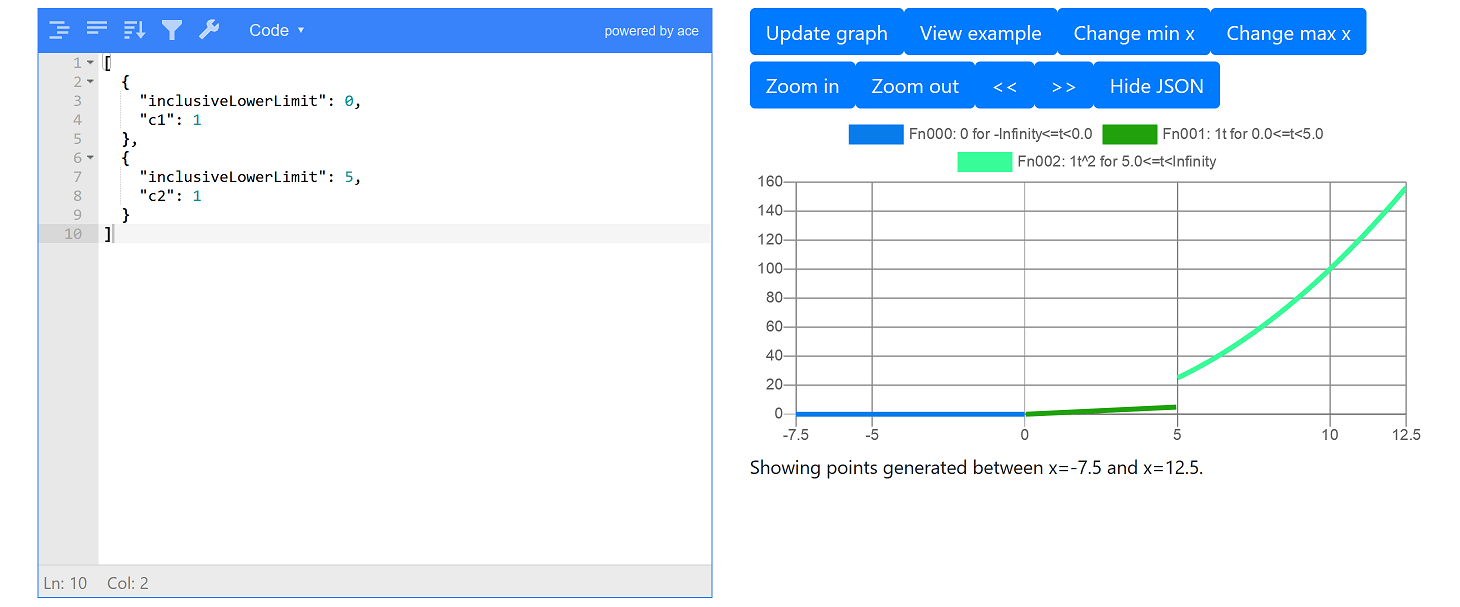
Here we see the function has 3 distinct parts: (a) 0 for x < 0, (b) linear for 0 ≤ x < 5 and (c) squared (i.e. quadratic) for x ≥ 5. We also see that the function jumps at x = 5. Generally you want to avoid jumps in your penalty functions, and penalty functions should always be increasing, they should not decrease.

The penalty function jumps because for the 1st subfunction p(5) = 1 × 5 = 5 and for the 2nd subfunction p(5) = 1 × 5² = 25. The easiest way to fix this jump is to add a field join to the 2nd subfunction and set its value to EXACT:

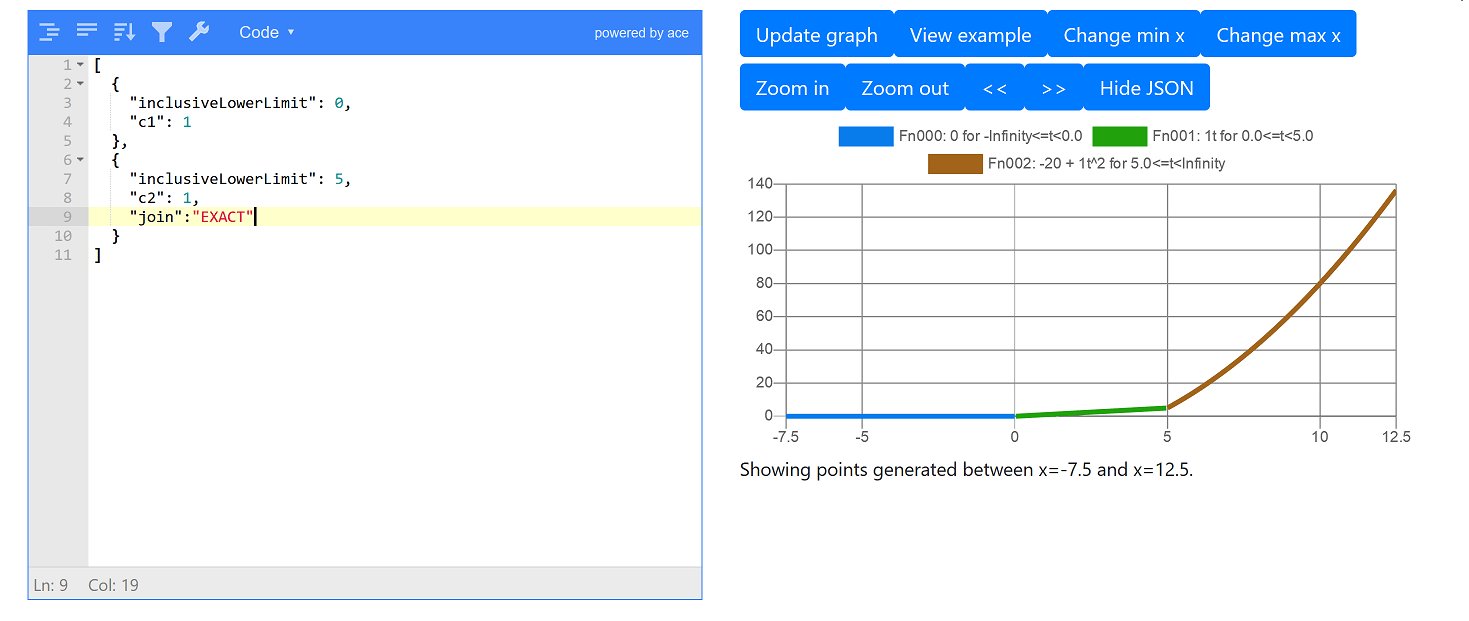
Setting join=EXACT in the 2nd subfunction tells ODL Live to automatically set the c₀ fixed cost constant in 2nd subfunction to match the last value of the 1st subfunction at the boundary between the two subfunctions. In other words, it tells ODL Live that the 2nd subfunction must join exactly with the end of the 1st subfunction.

Supported values of join are:

EXACT. Force the subfunction to match the end value of the preceeding subfunction.
PLUS_CONST. Force the subfunction to match the end value of the preceeding subfunction but then add the value of c₀ to the start point of the subfunction, so we have a jump in the cost function and you can easily set the size of the ‘jump’.
INCREASING. Ensure that the start of the subfunction is greater than or equal to the end of the last subfunction.
NO_JOIN. Do nothing (this is the same as omitting the join field).

Now let’s say we want the linear function to start at 2, so we set inclusiveLowerLimit=2:

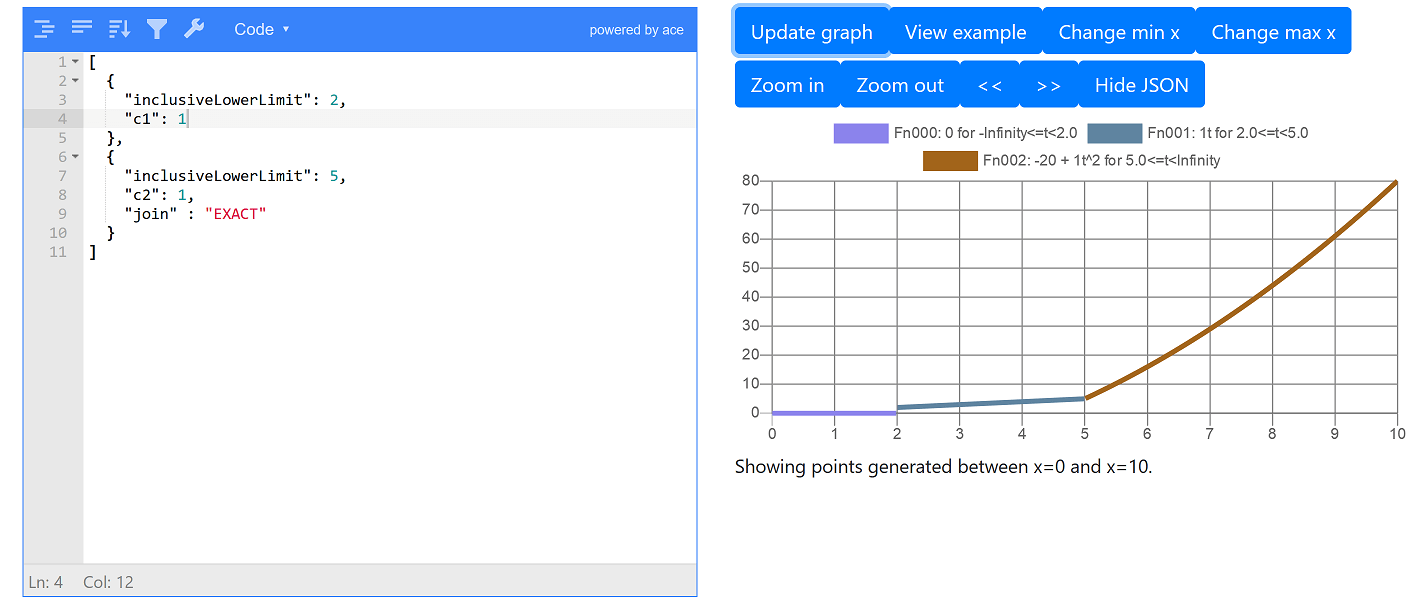
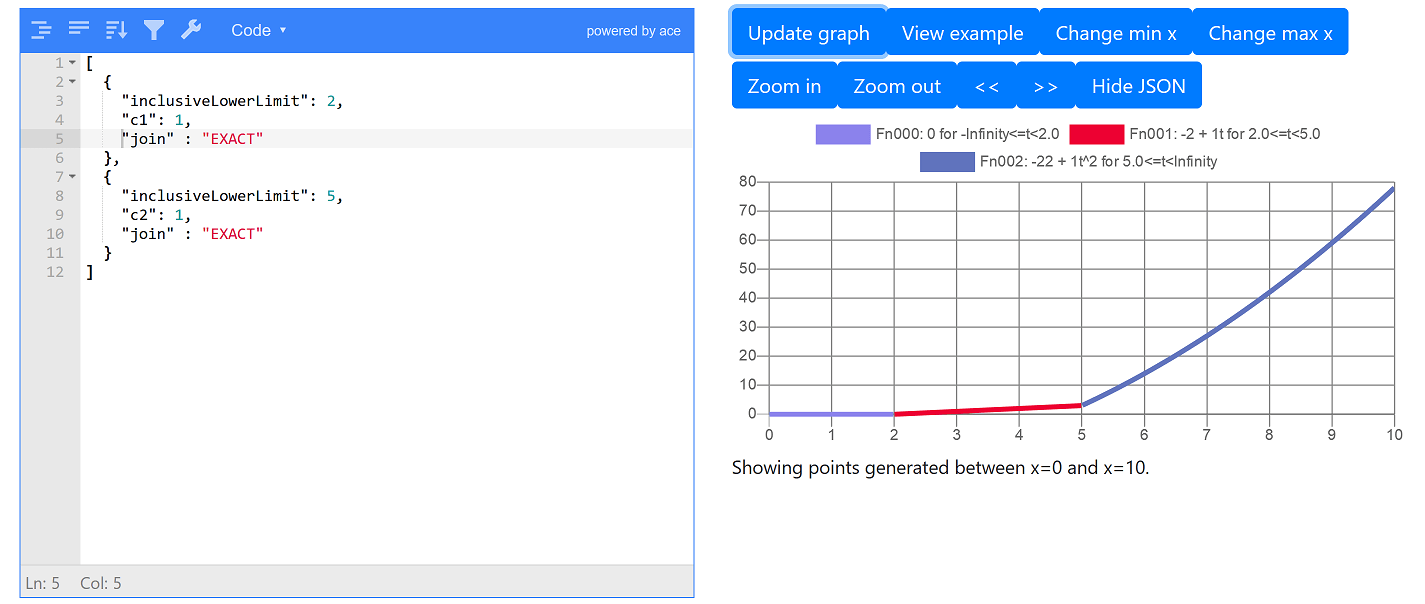
Again we get a jump at x = 2 as p(x) is always 0 before the 1st subfunction and the value of the 1st subfunction at x = 2 is p(2) = c₁ × 2 = 2. We can remove this jump by setting join to EXACT for 1st function too:

Another (possibly more complex) way to stop this jump would be to set translate on the 1st function to 2 instead, so we minus 2 from the value of x as follows:

[
  {
    "inclusiveLowerLimit": 2,
    "translate" : 2,
    "c1": 1
  },
  {
    "inclusiveLowerLimit": 5,
    "c2": 1,
    "join" : "EXACT"
  }
]

If we decided that we did want a jump at the start of the function (at x = 2) but we want to explicitly set what the initial value of the function will be, the easiest way to do this is to (a) set the initial value in the c₀ constant and (b) then set the join to be PLUS_CONST. As p(x) always equals 0 before the first subfunction, the join will set the value of the first function to be 0 + c₀. We this in the following screenshot where we’ve set the initial value at 20:

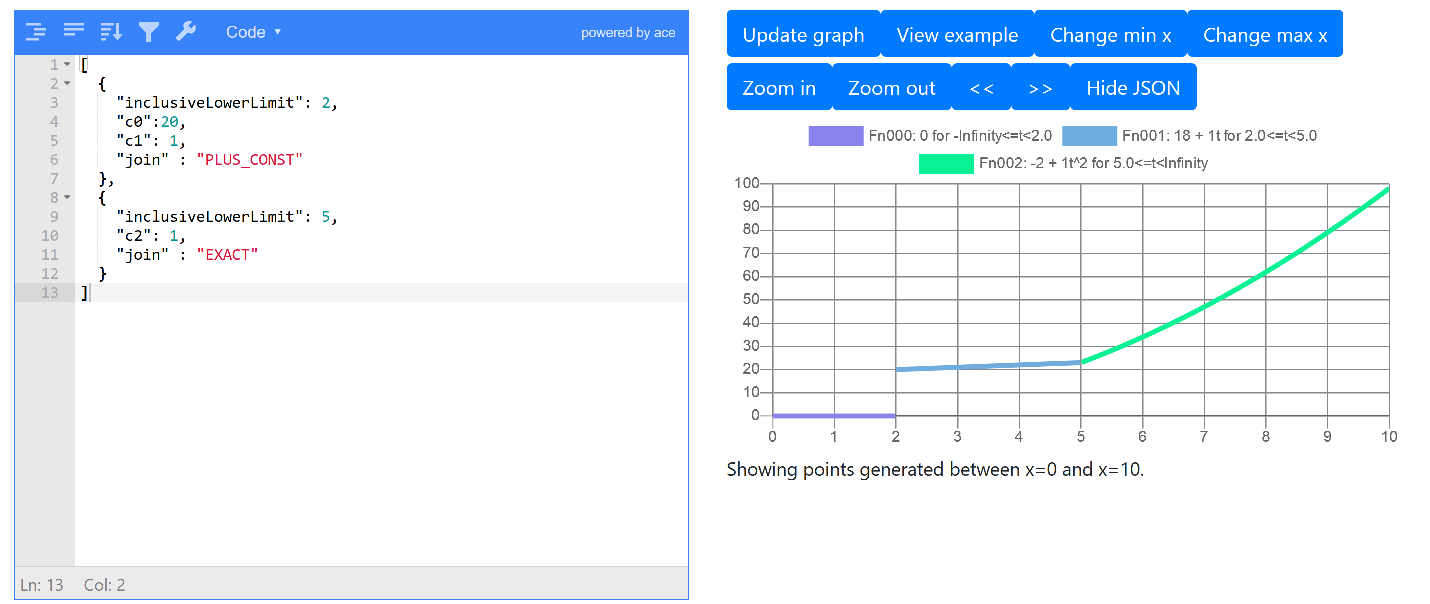
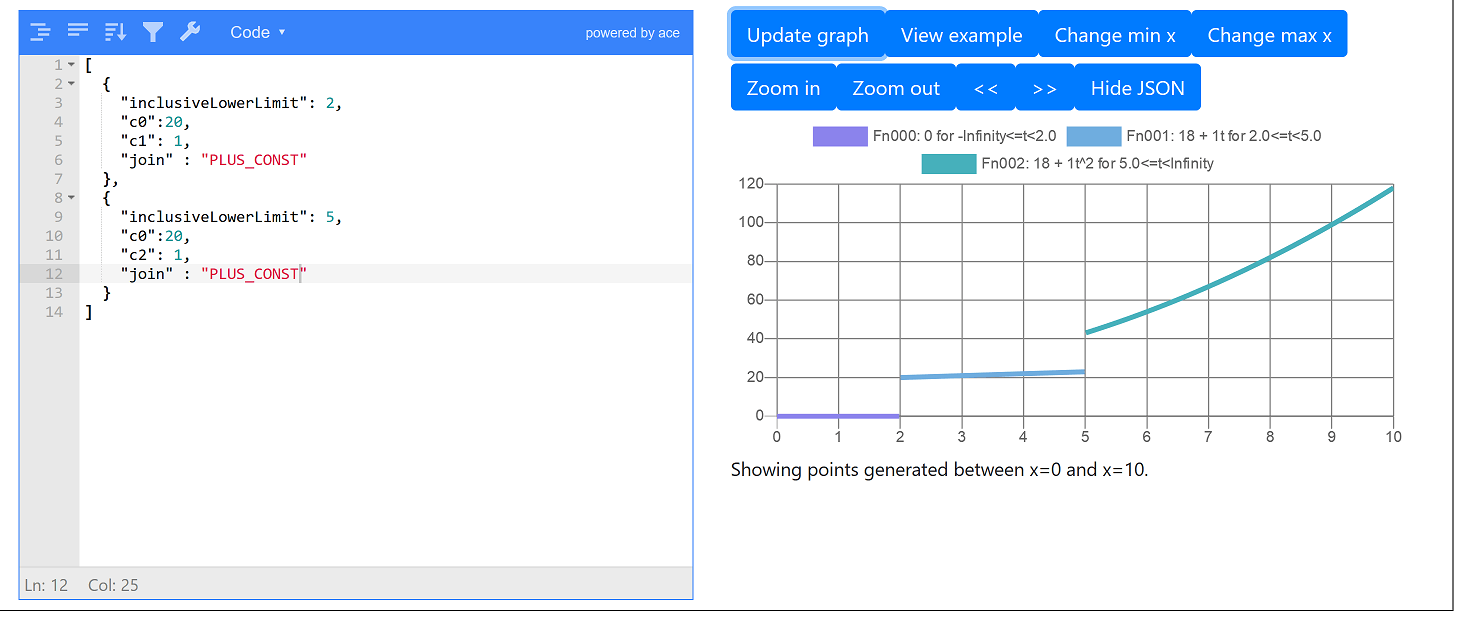
The same logic can apply for later functions as well. For example if we wanted a jump at x = 5 where the 2nd function starts we could set an explict jump of 20 there too:

We can also set that a range of x is prohibited, so that the optimiser won’t break this rule in the prohibited area and will instead leave one or more jobs unassigned. We do that in the following screenshot where we’ve added a 3rd function which has prohibited=true for x ≥ 10. The prohibited region is shown on the graph as the area filled with grey:

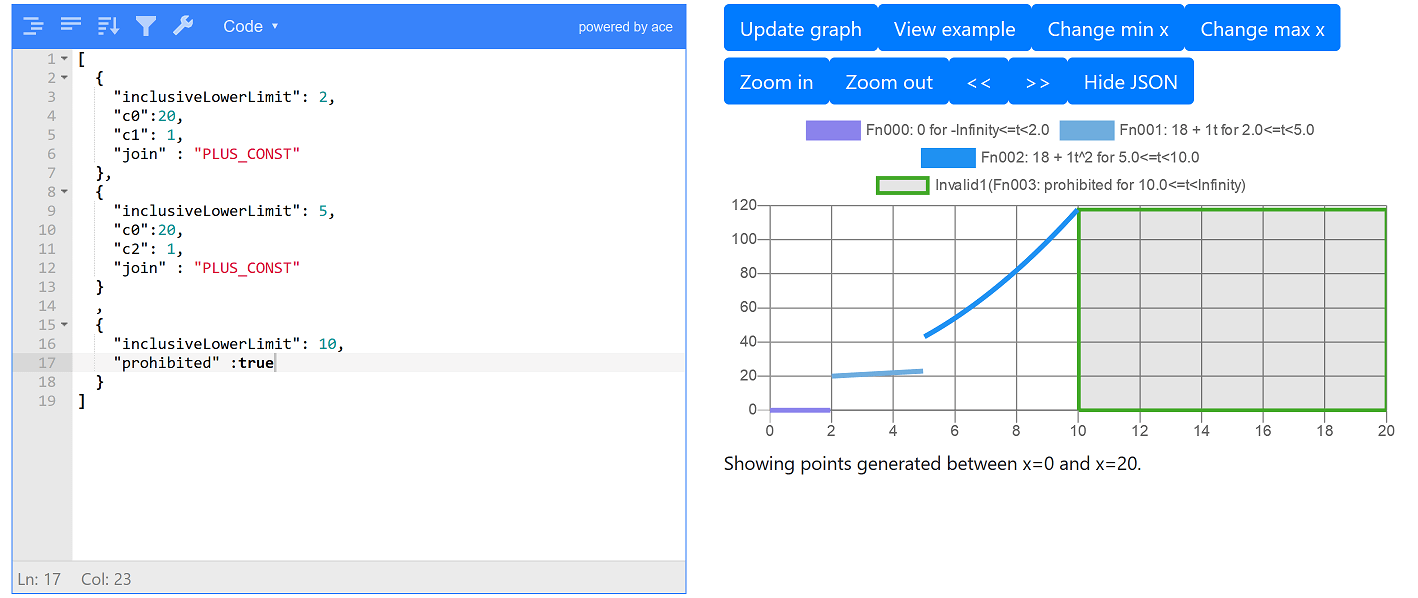
If this function was used for total travel hours, the optimiser would not allow a route to have more than 10 hours travel.